In the field of fluid mechanics, the Navier-Stokes equations are central to understanding fluid flow. However, these equations can only be solved analytically under limited conditions. For real-world engineering applications, we need to use numerical methods to approximate these solutions. This is where discretization in Computational Fluid Dynamics (CFD) becomes crucial.
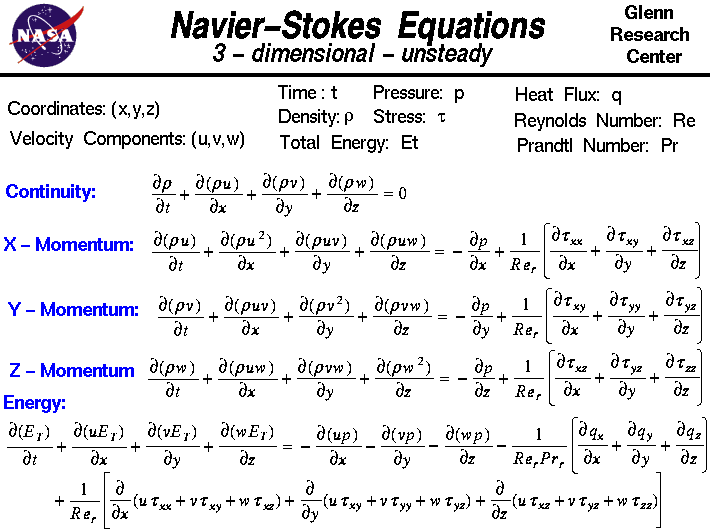
Table of Contents
What is Discretization in CFD?
Discretization is a technique used to convert the continuous partial differential equations (PDEs) that describe fluid flow into a system of algebraic equations. These algebraic equations can then be solved on a computer, making it possible to analyze complex fluid dynamics problems.
In simpler terms, discretization breaks down the fluid flow domain into smaller, manageable pieces (grid points or control volumes) where the equations are solved. This method allows for the numerical approximation of fluid flow at discrete points in space and time, providing a practical solution when analytical methods are insufficient.
Key Discretization Approaches in CFD
1. Finite Difference Method (FDM)
The Finite Difference Method is one of the oldest and simplest methods for discretizing PDEs. It approximates the derivatives in the equations using differences between function values at discrete grid points.
Basic Steps in FDM:
- Divide the domain into a grid with uniform or non-uniform spacing.
- Replace the partial derivatives in the PDEs with finite difference approximations.
- Solve the resulting system of algebraic equations to obtain the values of the dependent variables at each grid point.
2. Finite Volume Method (FVM)
The Finite Volume Method starts with the integral form of the conservation equations. The domain is divided into control volumes, and the conservation laws are applied to each control volume. This method is widely used in engineering because it conserves quantities like mass and energy within each control volume.
Basic Steps in FVM:
- Divide the domain into discrete control volumes.
- Apply the conservation equations to each control volume to form algebraic equations.
- Solve these equations to determine the variable values at the computational nodes, which are located at the centroids of the control volumes.

Special Considerations in Discretization
Discretization of Diffusion Fluxes
When dealing with diffusion processes in CFD, such as heat conduction (Fourier’s law) or fluid flow in porous media (Darcy’s law), the flux needs to be discretized carefully. The accuracy of these discretizations often depends on the grid structure and the method used to approximate the fluxes.
Approximation of Advection Terms
Advection terms, which describe the transport of quantities like momentum or energy within the fluid, are susceptible to the discretization method. Proper approximation of these terms is critical to ensuring the stability and convergence of the numerical solution.
Source Term Linearization
In the finite volume method, source terms that are non-linear functions of conserved variables must be linearized for proper discretization. A key rule in this process is to ensure that the linearized source term does not introduce positive coefficients that could destabilize the solution.
Conclusion: The Role of Discretization in CFD

Discretization is a fundamental step in solving fluid dynamics problems numerically. By breaking down complex equations into manageable pieces, it allows engineers and scientists to approximate fluid flow solutions that are otherwise impossible to obtain analytically. Understanding and correctly applying discretization methods like FDM and FVM is essential for accurate and stable CFD simulations.
References
- Anderson, J. D. (1995). Computational Fluid Dynamics: The Basics with Applications. McGraw-Hill Education. Source
- Versteeg, H. K., & Malalasekera, W. (2007). An Introduction to Computational Fluid Dynamics: The Finite Volume Method. Source
- Ferziger, J. H., & Peric, M. (2002). Computational Methods for Fluid Dynamics. Source

