In the realm of Computational Fluid Dynamics (CFD), the conservation equation is fundamental to modeling and predicting fluid behavior. These equations are based on the fundamental principles of conservation of mass, momentum, and energy, which govern the behavior of fluid flows. Understanding these equations is crucial for anyone involved in CFD, as they form the backbone of all fluid dynamics simulations.
Table of Contents
The Basics of Conservation Equations
Conservation equations are mathematical formulations that express the principle that certain properties of a physical system (such as mass, momentum, or energy) remain conserved over time within a defined control volume. In the context of CFD, these equations describe how these conserved properties change with time and space within a fluid.
The three primary conservation equations in fluid dynamics are:
- Conservation of Mass (Continuity Equation): This equation ensures that mass is neither created nor destroyed within a fluid system. It is expressed as:
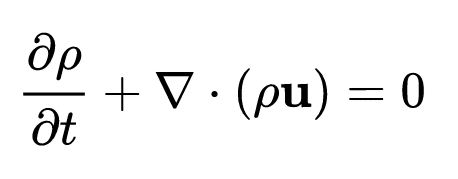
- Conservation of Momentum (Navier-Stokes Equation): This equation describes the change in momentum of the fluid particles as they move through the domain. It takes the form:
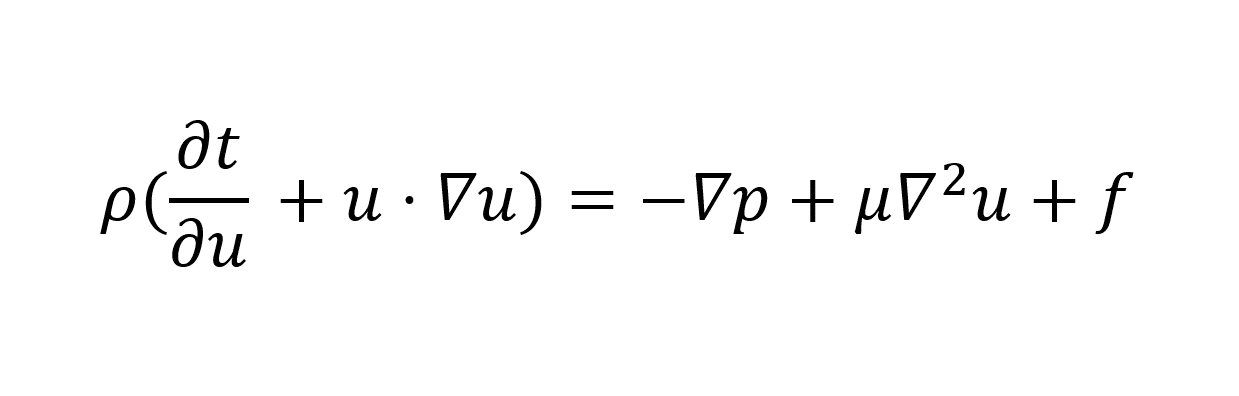
- Conservation of Energy: This equation accounts for the energy exchange within the fluid system due to heat transfer, work done by forces, and internal energy changes. The general form is:
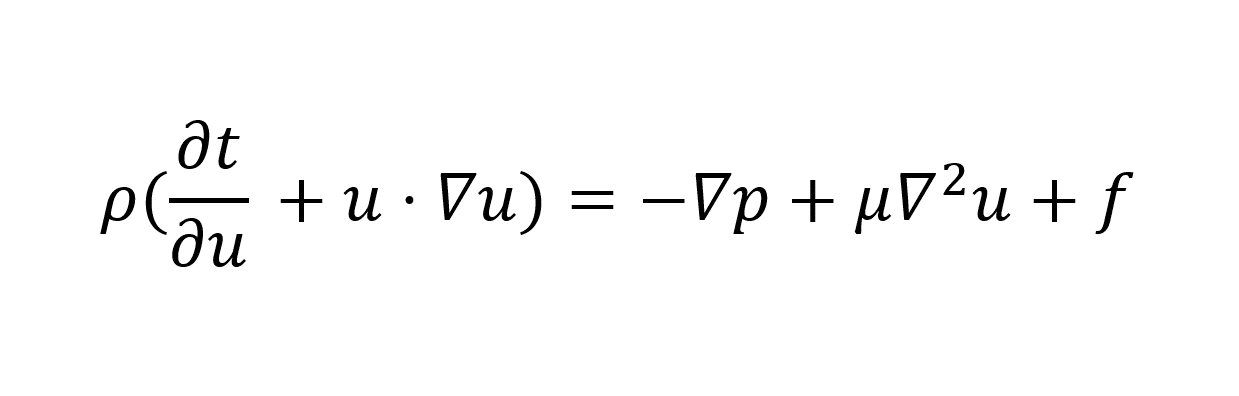
Why Conservation Equations Matter in CFD
The conservation equations are integral to CFD because they ensure that simulations accurately reflect the physical realities of fluid flow. Without these equations, it would be impossible to develop reliable models that predict how fluids behave under different conditions.
These equations form the basis of the mathematical models used in CFD software to simulate fluid flow. By solving these equations numerically, CFD practitioners can predict how fluids will move, how pressure and temperature will change, and how forces will interact within a fluid system. This is essential for designing and optimizing everything from aircraft and automobiles to HVAC systems and industrial processes.
Applications of Conservation Equations in CFD
The application of conservation equations in CFD spans a wide range of industries and disciplines:
- Aerospace Engineering: Predicting airflow around aircraft to improve aerodynamic efficiency.
- Automotive Engineering: Analyzing air and fuel mixtures in engines to enhance performance and reduce emissions.
- Environmental Engineering: Modeling pollutant dispersion in air and water to assess environmental impact.
- Industrial Processes: Designing efficient systems for heating, cooling, and fluid transport.
Each application relies on accurately applying the conservation of mass, momentum, and energy principles to ensure that the simulations provide meaningful results.
Conclusion: The Importance of Conservation Equations in CFD
In summary, conservation equations are the foundation of all fluid dynamics simulations in CFD. They ensure that the principles of mass, momentum, and energy conservation are adhered to, providing the necessary framework for accurate and reliable fluid flow predictions. Understanding these equations and how they are applied in CFD is essential for anyone looking to master the field of computational fluid dynamics.
References
- Anderson, J. D. (1995). Computational Fluid Dynamics: The Basics with Applications. McGraw-Hill Education. Source
- Versteeg, H. K., & Malalasekera, W. (2007). An Introduction to Computational Fluid Dynamics: The Finite Volume Method. Pearson Education. Source
- Ferziger, J. H., & Peric, M. (2002). Computational Methods for Fluid Dynamics. Source

