สมการ Navier-Stokes เป็นหัวใจสำคัญในการทำความเข้าใจการไหลของของไหล อย่างไรก็ตาม สมการเหล่านี้สามารถแก้ไขเชิงวิเคราะห์ได้เฉพาะในเงื่อนไขที่จำกัดเท่านั้น สำหรับการประยุกต์ใช้งานด้านวิศวกรรมในโลกแห่งความจริง เราจำเป็นต้องใช้วิธีเชิงตัวเลขในการประมาณคำตอบ นี่คือจุดที่การกระจายตัว (Discretization) ใน Computational Fluid Dynamics (CFD) เข้ามามีบทบาทสำคัญ
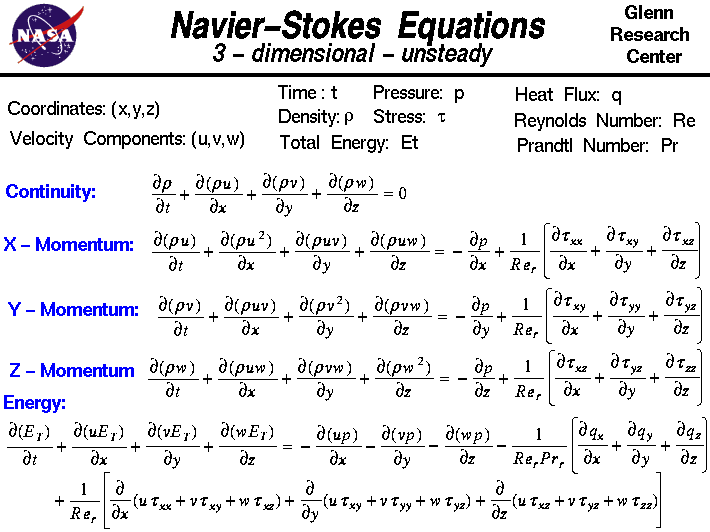
Table of Contents
การกระจายตัว (Discretization) ใน CFD คืออะไร?
การกระจายตัว (Discretization) เป็นเทคนิคที่ใช้ในการแปลงสมการเชิงอนุพันธ์บางส่วนแบบต่อเนื่อง (PDEs) ที่อธิบายการไหลของของไหลให้กลายเป็นระบบสมการเชิงพีชคณิต สมการเหล่านี้สามารถแก้ไขบนคอมพิวเตอร์ ทำให้สามารถวิเคราะห์ปัญหาการไหลของไหลที่ซับซ้อนได้
ในคำพูดที่ง่ายขึ้น การกระจายตัว เป็นการแบ่งโดเมนการไหลของของไหลให้เป็นชิ้นส่วนที่จัดการได้ง่ายขึ้น (จุดตารางหรือปริมาตรควบคุม) ที่ซึ่งสมการจะถูกแก้ไข วิธีนี้ช่วยให้สามารถประมาณการไหลของของไหลแบบเชิงตัวเลขที่ตำแหน่งและเวลาที่กำหนดได้ โดยให้ทางออกที่ปฏิบัติได้จริงเมื่อวิธีเชิงวิเคราะห์ไม่เพียงพอ
Key Discretization Approaches in CFD
1. Finite Difference Method (FDM)
วิธีต่างอนุพันธ์จำกัดเป็นหนึ่งในวิธีการที่เก่าแก่และง่ายที่สุดในการกระจายตัว PDEs มันประมาณอนุพันธ์ในสมการโดยใช้ความแตกต่างระหว่างค่าฟังก์ชันที่จุดตารางที่กำหนด
Basic Steps in FDM:
- แบ่งโดเมนเป็นตารางที่มีช่องว่างแบบสม่ำเสมอหรือไม่สม่ำเสมอ
- แทนที่อนุพันธ์บางส่วนใน PDEs ด้วยการประมาณค่าความแตกต่างจำกัด
- แก้ระบบสมการเชิงพีชคณิตที่เกิดขึ้นเพื่อให้ได้ค่าของตัวแปรที่ขึ้นอยู่ในแต่ละจุดตาราง
2. Finite Volume Method (FVM)
วิธีปริมาตรจำกัดเริ่มต้นด้วยรูปแบบเชิงปริพันธ์ของสมการการอนุรักษ์ โดยการแบ่งโดเมนออกเป็น ปริมาตรควบคุม และใช้กฎการอนุรักษ์ในแต่ละปริมาตรควบคุม วิธีนี้ใช้กันอย่างแพร่หลายในวิศวกรรมเพราะสามารถรักษาปริมาณเช่นมวลและพลังงานในแต่ละปริมาตรควบคุม
ขั้นตอนพื้นฐานใน FVM:
- แบ่งโดเมนออกเป็นปริมาตรควบคุมที่ไม่ต่อเนื่อง
- ใช้สมการการอนุรักษ์กับแต่ละปริมาตรควบคุมเพื่อสร้างสมการเชิงพีชคณิต
- แก้สมการเหล่านี้เพื่อกำหนดค่าตัวแปรที่จุดคำนวณ ซึ่งตั้งอยู่ที่จุดศูนย์กลางของปริมาตรควบคุม

ข้อพิจารณาพิเศษในการกระจายตัว
การกระจายตัวของฟลักซ์การแพร่กระจาย (Discretization of Diffusion Fluxes)
เมื่อจัดการกับกระบวนการการแพร่กระจายในการคำนวณ CFD เช่น การนำความร้อน (Fourier’s law) หรือการไหลในสื่อที่มีรูพรุน (Darcy’s law) ฟลักซ์ต้องได้รับการกระจายตัวอย่างระมัดระวัง ความแม่นยำของการกระจายตัวเหล่านี้มักขึ้นอยู่กับโครงสร้างของกริดและวิธีที่ใช้ในการประมาณค่าฟลักซ์
การประมาณค่าเทอมพาค (Approximation of Advection Terms)
เทอมพาค ซึ่งอธิบายการขนส่งปริมาณต่างๆ เช่น โมเมนตัมหรือพลังงานภายในของไหล มีความอ่อนไหวต่อวิธีการกระจายตัว การประมาณค่าเทอมเหล่านี้อย่างถูกต้องมีความสำคัญต่อการรักษาเสถียรภาพและการรวมกันของวิธีการเชิงตัวเลข
การแปรเชิงเส้นของเทอมแหล่งที่มา (Source Term Linearization)
ในวิธีปริมาตรจำกัด เทอมแหล่งที่มา (Source terms) ซึ่งเป็นฟังก์ชันไม่เชิงเส้นของตัวแปรอนุรักษ์ จำเป็นต้องแปรเป็นเชิงเส้นเพื่อการกระจายตัวที่เหมาะสม กฎสำคัญในกระบวนการนี้คือ การตรวจสอบให้แน่ใจว่าเทอมแหล่งที่มาเชิงเส้นไม่สร้างค่าสัมประสิทธิ์บวกที่อาจทำให้การแก้ปัญหาไม่เสถียร
สรุป: บทบาทของการกระจายตัวใน CFD

การกระจายตัวเป็นขั้นตอนพื้นฐานในการแก้ปัญหากลศาสตร์ของไหลแบบเชิงตัวเลข โดยการแบ่งสมการที่ซับซ้อนออกเป็นชิ้นส่วนที่จัดการได้ง่ายขึ้น มันช่วยให้วิศวกรและนักวิทยาศาสตร์สามารถประมาณการคำตอบการไหลของของไหลที่เป็นไปไม่ได้ในเชิงวิเคราะห์* การทำความเข้าใจและใช้วิธีการกระจายตัวอย่างถูกต้อง เช่น FDM และ FVM มีความสำคัญต่อการจำลอง CFD ที่แม่นยำและเสถียร
อ้างอิงจาก
- Anderson, J. D. (1995). Computational Fluid Dynamics: The Basics with Applications. McGraw-Hill Education. Source
- Versteeg, H. K., & Malalasekera, W. (2007). An Introduction to Computational Fluid Dynamics: The Finite Volume Method. Source
- Ferziger, J. H., & Peric, M. (2002). Computational Methods for Fluid Dynamics. Source










